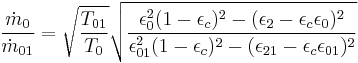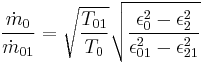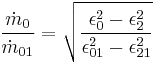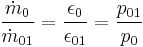Ellipse Law
The Law of the Ellipse, or Stodola's cone law,[1][2] attributed to Aurel Stodola, provides a method for calculating the highly nonlinear dependence of extraction pressures with a flow for multistage turbine with high backpressure, when the turbine nozzles are not choked.[3] It is important in turbine off-design calculations.
Contents |
Description
We consider a multistage turbine, like in the picture. The design calculation is done for design flow rate (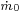 , the flow expected for the most uptime). The others parameters for design are the temperature and pressure at the stage group intake,
, the flow expected for the most uptime). The others parameters for design are the temperature and pressure at the stage group intake, 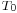 and
and 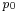 , respectively the extraction pressure at the stage group outlet
, respectively the extraction pressure at the stage group outlet 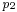 (the symbol
(the symbol 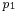 is used for the pressure after a stage nozzles, pressure does not interfere in relations here).
is used for the pressure after a stage nozzles, pressure does not interfere in relations here).
For off-design calculations, the off-design flow rate is 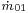 , respectively the temperature and pressure at the stage group intake are
, respectively the temperature and pressure at the stage group intake are 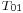 and
and 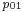 and the outlet pressure is
and the outlet pressure is 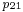 .
.
Stodola established experimentally that the relationship between these three parameters represented in Cartesian coordinate system has the shape of a degenerate quadric surface, the cone directrix being an ellipse.[4][5] For a constant initial pressure 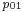 the flow rate depends on the outlet pressure
the flow rate depends on the outlet pressure 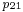 as an arc of ellipse in a plane parallel to
as an arc of ellipse in a plane parallel to 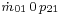
For very low outlet pressure 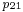 , like for condensing turbines, flow rates do not change with the outlet pressure, but drops very quickly with the increase of the backpressure. For a given outlet pressure
, like for condensing turbines, flow rates do not change with the outlet pressure, but drops very quickly with the increase of the backpressure. For a given outlet pressure 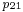 , flow rates changes depending on the inlet pressure
, flow rates changes depending on the inlet pressure 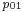 as an arc of hyperbola in a plane parallel to
as an arc of hyperbola in a plane parallel to 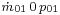 .
.
Usually, Stodola's cone do not represent absolute flow rates and pressures, but relative to the maximum flow rate and pressures, the maximum values of the diagram having in this case the value of 1. The maximum flow rate has the symbol 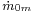 and the maximum pressures at the inlet and outlet have the symbols
and the maximum pressures at the inlet and outlet have the symbols 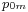 and
and 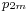 . The pressure ratios for design flow rate at the intake and outlet are
. The pressure ratios for design flow rate at the intake and outlet are 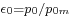 and
and 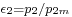 , and the off-design ratios are
, and the off-design ratios are 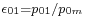 and
and 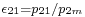 .
.
If in a stage is reached the speed of sound, the group of stages can be analyzed till that stage, which is the last in the group, the remaining stages forming another group of analysis. This division is imposed by the stage working in limited (choked) mode. The cone is shifted in the  axis direction, appearing a triangular surface, depending on the critical pressure ratio
axis direction, appearing a triangular surface, depending on the critical pressure ratio 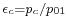 , where
, where 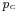 is the outlet critical pressure of the stage group.[6][7]
is the outlet critical pressure of the stage group.[6][7]
The analytical expression of the flow ratio is:[8]
For condensing turbine the ratio 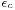 is wery low, previous relation reduces to:
is wery low, previous relation reduces to:
simplified relationship obtained theoretically by Gustav Flügel (1885–1967).[8][9]
In the event that the variation of inlet temperature is low, the relationship is simplified:
For condensing turbines 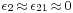 , so in this case:
, so in this case:
During operation, the above relations allow the assessment of the flow rate depending on the operating pressure of a stage.
References
- (Romanian) Gavril Creța, Turbine cu abur și cu gaze (English: Steam and Gas Turbines), Bucureşti: Ed. Didactică şi Pedagogică, 1981, 2nd ed. Ed. Tehnică, 1996, ISBN 973-31-0965-7
- (Romanian) Alexander Leyzerovich, Large Steam Power Turbines, Tulsa, Oklahoma: PennWell Publishing Co., 1997, Romanian version, București: Editura AGIR, 2003, ISBN 973-8466-39-3
Further reading
- (German) Aurel Stodola, Die Dampfturbinen, Berlin: Springer Verlag, 1903 - 1924 (six editions)
- Aurel Stodola, Steam and Gas Turbines, New York: McGraw-Hill, 1927
- (German) Constantin Zietemann, Die Dampfturbinen, 2nd ed., Berlin-Göttingen-Heidelberg: Springer-Verlag, 1955
- Walter Traupel, New general theory of multistage axial flow turbomachines. Translated by Dr. C.W. Smith, Washington D.C. Published by Navy Dept.
- Sydney Lawrence Dixon, Fluid Mechanics and Thermodynamics of Turbomachinery, Pergamon Press Ltd., 1966, 2nd ed. 1975, 3rd ed. 1978 (reprinted 1979, 1982 [twice], 1986, 1986, 1989, 1992, 1995), 4th ed. 1998
Notes
- ^ Timot Veer, Andreas Ulvestad, Olav Bolland, FRAME, a Tool for Predicting Gas Turbine Condition as well as Reability, Availability Performance, ASME/IGTI TURBOEXPO Conference 2004 June 14-17, Vienna, Austria, GT-2004-53770
- ^ TU Delft Cycle-Tempo, Reference guide, tudelft.nl, accessed 2010-11-29
- ^ D. H. Cooke, On Prediction of Off-Design Multistage Turbine Pressures by Stodola's Ellipse, J. Eng. Gas Turbines Power, July 1985, Volume 107, Issue 3, 596 (11 pages), doi:10.1115/1.3239778
- ^ Creța, p. 300
- ^ Leyzerovich, p. 175
- ^ Creța, p. 301
- ^ Leyzerovich, p. 176
- ^ a b Creța, p. 303
- ^ Leyzerovich, p. 174